Когда десятичная часть еще не была известна, великий Архимед нашел значение числа «пи» с точностью 99,9%. Он открыл метод, который стал основой для многих более поздних вычислений, нарисовав правильные многоугольники в круге и описав их вокруг него. В результате Архимед вычислил значение π как отношение 22/7≈3,142857142857143.
Окружность, круг. Число пи
Окружность — это множество точек на плоскости, равноудаленных от определенной точки, называемой центром.
Именно поэтому колесные транспортные средства движутся по прямой линии. Когда колеса вращаются, центры колес находятся на одинаковом расстоянии от земли.
Радиус — это отрезок, соединяющий центр окружности с одной из ее точек. Конечно, все лучи равны между собой.
Струна — отрезок, соединяющий две точки окружности. (От греческого chord — аккорд).
Струна — тип вторичноротых животных, характеризующийся эндодермальным осевым скелетом в виде струны, который в верхней форме заменяется позвоночником. По структуре и функции нервной системы хордовые занимают первое место среди всех животных. В мире насчитывается более 60 000 видов хордовых. Отрезок, соединяющий две точки определенной кривой (например, окружность, эллипс, парабола, преувеличение).
Диаметр — это нить, проходящая через центр круга. Это соответствует двум лучам света. Диаметр — наибольшая строна окружности.
Дуга — часть окружности между двумя точками. Две точки определяют две дуги.
Дуга — это часть кривой между двумя крайними значениями строки. Для замкнутых кривых (окружностей, эллипсов и т.д.) струна образует пару дуг с одинаковыми конечными точками по разные стороны струны.
Окружность — это часть плоскости, заключенная в окружность (включая ее центр).
Область — это часть окружности, ограниченная двумя лучами. Два луча определяют два сектора.
Отрезок — это прямая линия, пересекающая кривую в двух или более точках.
Сегмент — это плоская фигура, заключенная между кривой и ее струной.
Свойства хорд окружности
Если окружные углы принадлежат одной струне и вершины этих углов находятся на одной стороне этой струны, то они равны.
Если пара зарегистрированных углов лежит на одной струне, а вершины этих углов находятся по разные стороны этой струны, то сумма этих углов равна 180°.
Если окружной и центральный углы имеют одну и ту же строку и вершины этих углов находятся на одной стороне этой строки, то окружной угол равен половине центрального угла.
Наибольший центральный угол ограничен наибольшей струной, а наименьший центральный угол ограничен наименьшей струной.
Общая часть двух струн AB и CD в E дает отрезок, где произведение длин одной струны равно соответствующему произведению другой: $ AE \ cdot EB = CE \ cdotED$.
Число пи
Для всех окружностей отношение длины к диаметру окружности равно одному и тому же числу. Обычно это обозначается греческой буквой $ \pi$. $ \ pi = \ frac ld\ приблизительно 3.1415926\ приблизительно\ frac\ text< (2 знака после запятой) или >\ frac \ текст.< (6 знаков) >$
Это бесконечная ациклическая дробь.
Число пи происходит от первой буквы греческого слова, обозначающего окружность. Это означает «окружность» и периметр.
В случае с π греки использовали логический подход, превосходящий 22/7 на 1,2 мм. Китайцы нашли дробь 355/113, допустив ошибку всего в семь знаков после запятой.
Запомнить эти дроби очень просто. Напишите нечетные числа 1, 1, 3, 3, 5, 5, где первая половина — знаменатель, а вторая половина — числитель.
Геометрический смысл числа пи
длина окружности единичного диаметра.
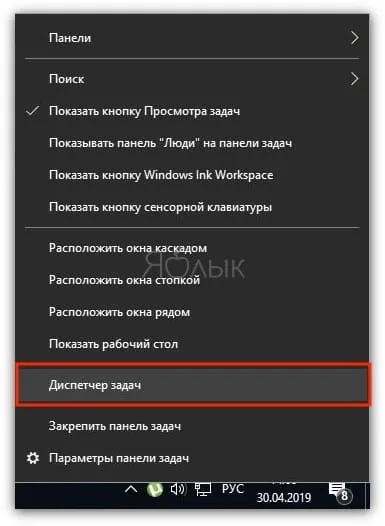
Циркуль и другие инструменты
Сегодня традиционный циркулярный компас не вызывает ни у кого уважения, поскольку конструкция из круга и арки гармонично вписалась в жизнь каждого из нас за школьной партой.
Компас — это инструмент для построения окружностей и дуг, его также можно использовать для измерения расстояний, особенно на картах.
Коза — это зажим для использования карандаша (ручки, носа, фломастера, кисти). Обычно компасы-козлы можно использовать для рисования окружностей карандашами, а также другими письменными принадлежностями, хотя точность обычного компаса значительно ниже.
Винтажная циркулярка — Рыцарь — Центр современного искусства M’ARS:.

Сгуститель — это компас с изогнутыми ножками для измерения объемных предметов.


Диабет имеет измерительный стержень (его название) с основной шкалой и вспомогательной шкалой для подсчета разделенных дробей. Принцип Нониуса основан на том, что, помимо всего прочего, он гораздо более чувствителен к шансу оценки, чем к относительной позиции оценки.
Компас ученика не может быть использован для построения больших окружностей. Однако мастеру может понадобиться изготовить круглые секции с очень большим диаметром. Самый простой вариант — любая рейка с гвоздем, встроенным в один конец, и отверстием для заостренного карандаша на другом конце на необходимом расстоянии. Если компас не используется, такой инструмент может работать достаточно хорошо, тем более что на разных расстояниях есть много отверстий для карандаша, чтобы спроектировать круг и дугу нужного размера.
Уровень (механический интегральный) — это инструмент для механического определения замкнутой контурной поверхности (готовой), спроектированной на плоской поверхности.
Принцип работы основан на измерении дуги, описываемой на поверхности специальным цилиндром. Цилиндр закреплен на одном из прозрачных рычагов простого механизма пантографа. Известное положение цилиндра с точки зрения звена механизма может быть достигнуто путем поворота стоимости из цилиндра в каждый конкретный момент времени по дуге со строго заданным радиусом, при закруглении контура, измеряемой в прямоугольном прямоугольнике с известной длиной и площадью. Она равна измеренной площади контура.
Построения
Как нарисовать окружность без циркуля
Найти центр окружности
Центр окружности является точкой пересечения двух диаметров.
Сгибание листа
Самый простой способ найти центр круга — сложить спроектированный лист бумаги и убедиться, что цикл сложен посередине. Полученная линия сгиба будет одним из диаметров области. Поскольку лист может изгибаться в противоположном направлении, вы получаете второй диаметр. Точка пересечения будет центром окружности. Конечно, этот метод полезен только в том случае, если цикл разработан на бумаге. Бумагу можно складывать и проверять точность складывания на свету.
Двусторонняя линейки
Если вы знаете, что ширина линейки меньше диаметра круга, используйте линейки с обеих сторон, чтобы начертить центр определенного круга.
Дополните полученную таблицу треугольником (углом), проведя две параллельные линии, пересекающие окружность, соединив вершину угла с точкой пересечения диагоналей трапеции. Затем повторите построение для получения второго диаметра.
Линейка с делениями
Поместите линейку на окружность и отметьте нулевым маркером любое место на окружности. Таким образом, измерьте вторичный отрезок, то есть отрезок, соединяющий две точки окружности. Затем медленно вращайте линейку и следите за изменением ширины участка. Вторичная увеличивается до тех пор, пока не станет диаметром, а затем снова начинает уменьшаться. Обратите внимание на диаметр и, следовательно, на максимальную точку, в которой находится центр.
Угольник
В случае прямоугольного треугольника центр периметра совпадает с центром субъекта. Так, если прямоугольный треугольник записан в круге, то его гипотенуза будет диаметром этого круга. В качестве трафарета для этого метода подойдет прямой угол — школьный или строительный уголок, или просто бумага. Поместите вершину прямого угла в любую точку цикла и отметьте точки, в которых стороны угла пересекают границы цикла. Это последние точки диаметра. Используя тот же метод, найдите второй диаметр. Точка их пересечения — центр окружности.
Циркуль
1. диаметр — это вид деления окружности. Выберите любую точку на окружности и с помощью компаса отметьте еще две точки на окружности, равные выбранной точке. Затем найдите точку, равную двум точкам. Соедините начальную и конечную точки — это и есть диаметр.
2. нарисуйте любую нить и постройте центральную вертикаль. Это диаметр.
Касательная к окружности
Вас просят построить касательную к окружности, причем касательная должна проходить через определенную точку.
Если местоположение знака не указано, необходимо рассмотреть три возможных случая положения точки.
Если точка находится в круге окружностей, то касательная к этой точке не может быть проведена.
Если точка находится в окружности, то касательная строится перпендикуляром, прямым к радиусу, проведенному через точку.
Если точка находится вне окружности, примыкающей к ней, найдите точку окружности, через которую должна пройти касательная.
Постройте отрезок, соединяющий центр окружности в этой точке. Затем проведите среднюю точку по вертикали. Затем нарисуйте круг (или его часть) с радиусом, равным половине сечения. Пересечение заданного цикла и спроектированного цикла является точкой контакта. Касательная линия проходит через две известные точки. Нет нужды говорить, что таких касательных две.
На самом деле, однако, эта концепция существует уже более 4 000 лет. Кроме того, древнеегипетские математики подтвердили, что длина окружности до ее диаметра одинакова в каждом цикле. Значение превышает 3.
Все окружности похожи
При сравнении окружностей разных размеров можно заметить, что Различные размеры круга пропорциональны. Это означает, что если диаметр круга увеличивается в раз, то его длина также увеличивается в раз. Математика может быть записана следующим образом: .
| C 1 | C 2 | |
| = | ||
| d 1 | d 2 | (1) |
где C1 и C2 — длины двух различных циклов, а D1 и D2 — диаметры. Эта связь работает при наличии коэффициента пропорциональности — уже известной константы P. Из соотношения (1) можно заключить, что длина окружности c равна произведению диаметра этого цикла на коэффициент цикла P.
Этот тип можно записать и в другой форме, выразив диаметр D в терминах радиуса r этого цикла.
Этот человек — проводник в мир кругов для учеников седьмого класса.
С древних времен люди пытались определить значение этой константы. Например, жители Месопотамии вычисляли площадь круга по следующей формуле:.
| C 2 | ||
| S | = | , |
| 12 |
где S — площадь круга, C — длина круга. Эта формула заменяет уже известную студентам формулу площади круга S = πr2 и длины окружности C = 2πR, которая имеет вид
| (2 π R) 2 | |
| π R 2 | = |
| 12 |
В Древнем Египте значение π было более точным. 2000-1700 ГГ. ДО Н.Э. Писец по имени Эймс написал папирус. Там вы найдете рецепты для решения различных практических задач. Например, использование математических формул для нахождения площади круга:.
| 8 | 2 | |||
| S | = | ( | d | ) |
| 9 |
Какая идея пришла в голову этому человеку? — Мы не знаем. Вероятно, она основана на его наблюдениях, как это делали и другие древние философы.
По стопам Архимеда
-Какое из двух чисел больше 22/7 или 3,14? -Они равны. — Почему; — каждый из них равен p. Из анкеты обследования А. А. Власова.
Некоторые люди считают, что дробь 22/7 и число пи — это одно и то же. Однако это неверно. Кроме вышеперечисленных неправильных ответов на экзамене (см. надпись), в эту группу можно добавить очень веселую загадку. Задание заключается в следующем. ‘Переставьте спички так, чтобы уравнение стало верным’.
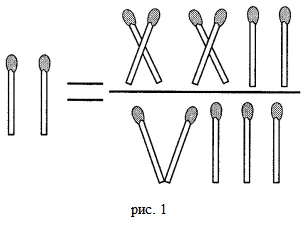
Решение заключается в следующем. Используйте одну из вертикальных спичек в правом знаменателе для формирования «крыши» из двух вертикальных спичек слева. Возникает визуальное представление буквы π.
Многие знают, что приближение π = 22/7 было определено древнегреческим математиком Архимедом. В честь этого приближение часто называют «числом Архимеда». Архимед не только определил приближение к π, но и нашел точность этого приближения. Другими словами, он смог найти узкий арифметический интервал, которому принадлежит π. В одной из своих работ Архимед доказывает цепь неравенств, видимых в современном виде. Например, так:.
| 10 | 6336 | 14688 | 1 | |||
| 3 | | π |
3 |
| |||
| 71 | 1 | 1 | 7 | |||
| 2017 | 4673 | |||||
| 4 | 2 | |||||
Его можно записать проще: 3 140 909.< π < 3,1 428 265.
Как видно из неравенств, Архимед нашел достаточно точные значения с точностью до 0,002. Удивительно, но он нашел два знака после запятой: 3,14 — значение, которое чаще всего используется в простых расчетах.
Практическое применение
Два человека в поезде: «Смотри, рельсы прямые, а колеса круглые. Откуда исходит шум? -Что вы имеете в виду? Колеса круглые, а площадь круга равна квадрату пирса, так что квадратный удар!».
Как правило, люди соприкасаются с этим удивительным числом в 6-7 классах, но в конце 8 класса оно рассматривается более подробно. В этой части статьи мы представим основные и наиболее важные типы решения геометрических задач. Во-первых, для упрощения расчетов пусть π будет 3,14.
Возможно, самой популярной формулой среди студентов, использующих π, является формула для длины и площади круга. Первое уравнение для площади круга записывается следующим образом:.
| π D 2 |
| S= π R 2 = |
| 4 |
где S — площадь круга, R — его радиус, а D — диаметр круга.
Периметр окружности, иногда называемый длиной окружности или периметром круга, вычисляется по формуле
C=2πR=πd,.
где C — окружность круга, R — радиус, а d — диаметр круга.
Ясно, что диаметр d равен двум радиусам R.
Из формулы для окружности легко найти радиус круга.
| C | C |
| R= | = |
| 2 π | d |
Символизм этих типов остается неизменным.
Диаметр окружности можно найти по следующей формуле
| C | |
| D= | = 2R |
| π |
где D — диаметр, C — длина окружности, а R — радиус круга.
Это лишь некоторые из доступных программ для совместного использования для постановки целей. В некоторых случаях необходимо вычислить площадь не всего круга, а только его части, т.е. сектора. Поэтому существует формула для расчета площади вентилятора. Это происходит следующим образом.
| α | ||
| S | = | π R 2 |
| 360 ˚ |
Где S — площадь сектора, R — радиус круга, а A — центральный угол градуса.
Школьные учебники: математика 6 класс Мерзляк, параграф 24 Colo I длина окружности, площадь круга — геометрия 9 класс Мерзляк, параграф 2 многоугольник
Что особенного в числе Пи?

Номер PI, фото: социальные сети
Всего через две недели знаменитое число P отметит свой день рождения. Ученые продолжают говорить о нем, снимать его на пленку и постоянно использовать в своей высшей математике. Празднование мирового номера состоится 14 марта в 1:26 утра. Любителям математики не составит труда понять, почему этот весенний день считается именным. А для тех, кто не знает, но хочет узнать ответ на загадку и особенности P, наша статья будет очень полезна.
Прежде чем перейти к основным вопросам, давайте посмотрим на самые большие цифры. В 2011 году американский ученый в очередной раз установил мировой рекорд, подсчитав количество 10 триллионов «пи». Предыдущий рекорд был установлен теми же американскими и японскими экспертами, но с числом в пять триллионов. Конечно, математики не могли запомнить последовательность из десяти триллионов цифр. И им это не нужно. Для вычисления диаметра окружности достаточно знать 39 цифр.
Число P — это история.
У этого знака Зодиака есть несколько интересных особенностей.
- Чему равен число Пи?
- Сколько чисел после запятой в числе Пи?
- Как получить число Пи?
Интересное событие: в
В марте 2011 года американский музыкант Майкл Блейк решил создать мелодию из номера PI. Он составил его. Чтобы эксперимент прошел успешно, композитор взял 31 цифру после запятой. Он должен был перейти в следующую октаву, в каждой из которых была своя нота. С помощью цикла пентаграммы он присвоил каждой цифре свою строку. Мелодия размещается в темпе 157 ударов в минуту. Получилась очень интересная и шумная мелодия. Его можно найти в любом источнике в Интернете.
Число Пи, что такое? Его краткая история
Число II — это математическая константа. Она равна отношению длины окружности к длине ее диаметра. Название P было предложено английским математиком Джонсом в 1706 году; в 1737 году P приобрело формальное название благодаря математику Леонгарду Эйлеру.
На самом деле, однако, эта концепция существует уже более 4 000 лет. Кроме того, древнеегипетские математики подтвердили, что длина окружности до ее диаметра одинакова в каждом цикле. Значение превышает 3.
Архимед, Ханн и Ариабхата были искусными математиками и с годами приблизили число PI к его точной цене. Однако самое точное число было открыто китайским математиком Цзу Чунчжи в 480 году. В то время их количество составляло около 10 мест. Рудольф из Голландии смог назвать еще 20 цифр. Это отняло у него 20 лет жизни. Позже археологи нашли дневник, в котором были указаны следующие 15 цифр. К 1500 году цена на ПИ составляла уже 35 знаков.
Как только люди приобрели компьютерные системы, их стоимость стала резко возрастать. После запятой числа увеличиваются до триллионов.
Число Пи, особенности и факты
-
Никому, никогда не удастся узнать точное значение данной цифры. Почему? – это иррациональное число и его можно раскрыть только в бесконечной форме непериодической десятичной дроби.
-
Сколько число Пи и побит ли рекорд 2005 года? – Рекорд побит жителем Индии Мине. Он смог назвать 70.000 символов. Неофициально невероятный успех повторила девушка Акира Харагуи. Ей удалось назвать 100.000 знаков, но рекорд не был засчитан, поскольку не было эксперта Гиннеса.